Total number of incoming packets
Next we will study how the number of incoming packets affect the estimation of the estimation of the proportion of dropped packets. You can reproduce the results by running the following command:
# Point to your pcap
pcap=../pcaps/equinix-chicago.dirB.20130529-135900.UTC.anon.pcap
for ID in {1..100}
do
python estimate-ratio.py packets.$ID $pcap --rows ROWS --columns COLUMNS \
--maxIter 100 --averageFunction mean --hashFunction default \
--xiFunction default --dropProbability PDROP --digestSize 32
doneSmall ratio of dropped packets
Our first figure shows the 99% percentile of the error for intervals of different lengths. As we can see, the percentile soon becomes steady.
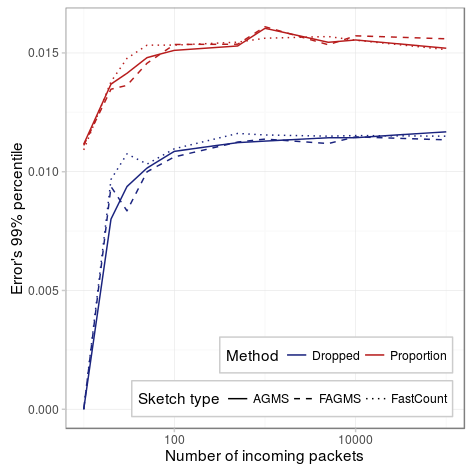
| Parameter | Value |
|---|---|
| Packets | {10,20,30,50,100,500,1000,5000,1e4,1e5} |
| Drop probability | 10% |
| Columns | 32 |
| Rows | 32 |
| Digest size | 32 |
| Hash function | default |
| Xi function | default |
| Pcap | CAIDA |
| Average function | mean |
Large ratio of dropped packets
For a larger amount of dropped packets, we see that the 99% seems constant regardless of the number of packets. Comparing with the figure above, we can see that now, estimating both the incoming and dropped packets provides a more accurate estimation, as we saw in the previous page.
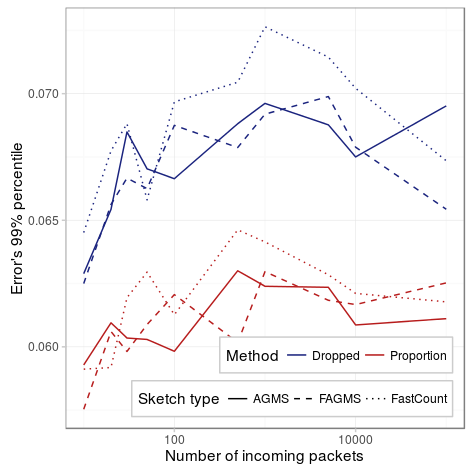
| Parameter | Value |
|---|---|
| Packets | {10,20,30,50,100,500,1000,5000,1e4,1e5} |
| Drop probability | 60% |
| Columns | 32 |
| Rows | 32 |
| Digest size | 32 |
| Hash function | default |
| Xi function | default |
| Pcap | CAIDA |
| Average function | mean |
Conclusions
The results of this experiments seem to be inline with the fact that the standard error of predicting the total number of packets is proportional to the value being estimated; since now we are estimating a proportion, the error should be constant, as the linear term is canceled out.